На 64 палях (“Настаўніцкая газета” за 25.10.2008г.)

Зоркі першай і другой велічыні

Імі сталі школьнікі бабруйчанка Марыя Хвашчынская і мінчанка Марыя Міронава на чэмпіянаце свету па шашках-64 сярод юніёрак, што ладзіўся ў г. Новаявораўск (Україна), а таксама мінчанін Уладзіслаў Кавалёў, які быў другім у г. Нові-Герцог (Чарнагорыя) на першынстве Еўропы па шахматах у намінацыі юнакоў да 14 гадоў. Добра выступілі і шахматысты Антон Шарамет з Асіповічаў (8-е месца ў групе ўдзельнікаў да 10 гадоў) і студэнт БНТУ Кірыл Ступак (такое ж месца, але ў старэйшай узроставай катэгорыі да 18 гадоў), дзе званне чэмпіёна кантынента заваяваў іспанец Ксавье Віла. Сталічная ж гімназістка Дар’я Федаровіч па выніках выступленняў на чэмпіянатах Еўропы і свету атрымала званне міжнароднага майстра. Яна – двухкратная чэмпіёнка краіны па шашках-64 сярод жанчын.

Бліцконкурсы

№ 9-5. Белыя: Крh5, Фa2, Ca1, Ca8 (4). Чорныя: Kpg3, пп. f5, h3 (3). Мат за 2 хады. Аўтар

– інжынер па будаўніцтву аддзела адукацыі Яўген Красоўскі (Мядзел).

№ 10-2. Белыя: a5, b4, b6, d6, e1, e7, g5 (7). Чорныя: c3, d2, d4, e3, f8, g3, g7 (7).

Выйгрыш. Склаў Дзмітрый Камчыцкі – наш чытач з Магілёва. Іх пераможцы будуць адзначаны. Адказы накіроўвайце на адрас: 220013, г. Мінск, пр. Незалежнасці, 77, рэдакцыя “Настаўніцкай газеты”, рубрыка “На 64 палях”.

Казачная задача

Яна належыць мінчаніну Дзмітрыю Кульбанаву. У ёй удзельнічаюць не толькі шахматныя фігуры, але і шашачныя:

Белыя: Kpg5, дамкі c7, f4, простая шашка d2 (4). Чорныя: Kpd4, Лb3, Лf2, Cc4, Cc5, пп.d3, d5, e2, e4, e7, f3 (11). Мат за 2 хады: 1. De5+ Лc3A 2. d2:f8x. A1… Kpe3 2. Dg3x. Але мызноў бачым, што ў задачы ўсяго два варыянты, а сучасная практыка шахматных двуххадовакпатрабуе, каб у іх было больш разгалінаванняў. Так што ёсць сэнс папрацаваць і ўдасканаліць твор Д. Кульбанава. Чакаем вашых варыяцый. Лепшыя з іх будуцьнадрукаваны.

Нашы лаўрэаты

У мінулы раз мы прывялі кампазіцыю на 100-клетачнай дошцы дырэктара Ходасаўскай сярэдняй школы Мсціслаўскага раёна, нацыянальнага майстра спорту Аляксандра Сапегіна, якая прынесла яму званне лаўрэата ў катэгорыі В міжнароднага конкурсу памяці чэмпіёна СССР мінчаніна Гары Далідовіча. Услед за А. Сапегіным фінішыраваў яшчэ адзін наш земляк – міжнародны гросмайстар Уладзімір Матус, які зараз жыве і працуе ў Маскве. Пазнаёмцеся і з яго находкай:

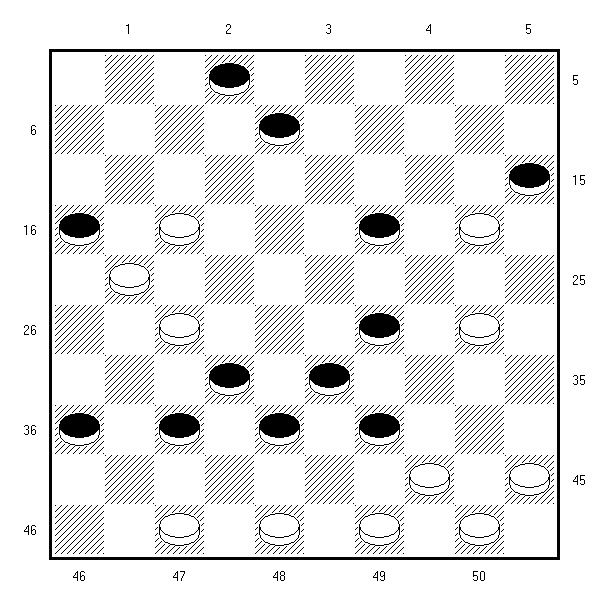
Белыя: 17, 20, 21, 27, 30, 44, 45, 47, 48, 49, 50 (11). Чорныя: 2, 8, 15, 16, 19, 29, 32, 33, 36, 37, 38, 39 (12). Змест: 11, 7, 47-42, 38 (27) 45-40, 2, 41х.

У сваю чаргу У. Матус перамог у катэгорыі С. Дарэчы, яго родны брат Віктар Паўлавіч Матус узначальвае аддзел народнай адукацыі Полацкага райвыканкама і старадаўняя гульня яму таксама спадабаецца.

Рашаем разам

Бліц-9/4 (В. Жылко): 1. Kpb6 Ce6 2. Kpa6 Kpc7 3. Cb5 Cc8x. 1… Kpb7 2. Kpd7 Kpb6 3. Kpc8 Ce6x. Блізнец: 1. Лb3 c7 2. Лb8+ cbФ 3. Kpc6 Фc7x. Бліц-10/1 (М. Стэфановіч): 1. cd8 2. da5 3. ab2 4. a:h8 (“слупняк” на вялікай дарозе!)х. Па-за конкурсам (М. Стэфановіч): № 3. 1. hg5 2. gf6 3. gf4 4. cb8 5. b8:f4:c1:a3:f8:h6:e3 (“турэцкі” удар!) 6. g:e3 (апазіцыя!)х.

Папярэднія заданні выканалі: настаўнік гісторыі А. Т. Янчук і яго выхаванцы Юлія Шукайла, В. Жук і В. Сіўругін (Камянец), А. Перавознікаў і У. Сапяжынскі (Рагачоў), А. Андрыяшка (в. Гошчава Івацэвіцкага раёна), І. Астроўскі і В. Касцян (Мінск), М. Агейка (Ганцавічы), У. Бандарык (в. Лугавая Слабада Мінскага раёна), Аляксандра Камінская (Вілейка), К. Козел (в. Ласосна Гродзенскага раёна), настаўніца фізкультуры М. Я. Лічко і яе вучні Анжаліка Кашкан, Я. Казлоў, Д. Мамедаў, А. і А. Яраховічы (в. Возера Уздзенскага раёна), Л. Жыхар (Мядзел), Д. Камчыцкі (Магілёў), Л. Буйло (г. п. Смілавічы Мінскага раёна), А. Емельянаў з Глуска (класіфікацыйны-64/8-12) і інш. З бліцамі-8/5-6 і 9/1-3 справіліся Я. Красоўскі (Мядзел), А. Янчук, В. Жук, Ю. Шукайла, В. Сіўругін, М. Агейка, І. Астроўскі, К. Козел. Сярод іх Леанід Жыхар у класіфікацыйным-64/12 (Г. Пятровіч) у варыянце A4… ed6 звярнуў увагу i на 7. fe3=, а Іван Астроўскі – на 1. Фf1x у заданні № 2 бліца-9 (М. Быкаў). Апошні прывёў рашэнне задачы М. Агейкі (1. а8Ф! Cf3+AB 2. Kp:f3 Kp:h3 3. Фh8x. A1…C:g4 2. Фe4 Kph5 3. Фh7x. B1… Cc2 2. Фh8+ Ch7 3. Ф:h7x), якая з’яўляецца варыяцыяй бліца-8/5. Аднак, як удакладніў яго аўтар П. Шклудаў, у ім на f5 павінна быць чорная пешка.

Мікалай ГРУШЭЎСКІ.